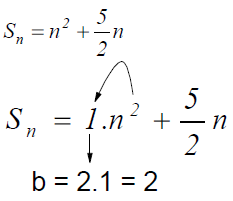Sifat dan Rumus Bangun Ruang KUBUS

Sifat dan Rumus Bangun Ruang KUBUS - Pada kesempatan kali ini, kita akan membahas tentang salah satu jenis bangun ruang sisi datar yakni kubus. Kubus merupakan bangun ruang tiga dimensi yang dibatasi oleh enam bidang sisi yang kongruen/ sama berbentuk bujur sangkar.

Bentuk Kubus

AF = Diagonal Bidang
AG = Diagonal Ruang

Beberapa Contoh Jaring-jaring Kubus

Sifat-sifat Kubus

1. Memiliki 6 buah sisi berbentuk persegi (bujur sangkar)
   (ABCD, EFGH, ABFE, CDHG, ADHE dan BCGF)
2. Memiliki 12 rusuk yang sama panjang
   (AB,BC,CD,DA,EF,FG,GH,HE,EA,FB,HD,GC)
3. Memiliki 8 titik sudut yang sama besar (siku-siku)
   (∠A, ∠B, ∠C, ∠D, ∠E, ∠F, ∠G, ∠H)
4. Mempunyai 12 diagonal bidang yang sama panjang
   (AC, BD,EG,HF,AF,EB,CH,DG,AH,ED,BG,CF)
5. Mempunyai 4 diagonal ruang
   (AG,BH,CE,DF)

Rumus Kubus

Volume   = sisi x sisi x sisi = s3
Luas     = 6 x sisi x sisi    = 6s2
Keliling = 12 x s
Diagonal bidang = s√2
Diagonal ruang  = s√3

Mungkin itu saja informasi yang bisa saya berikan tentang Sifat dan Rumus Bangun Ruang KUBUS semoga bermanfaat buat kalian semua.

Bangun Datar: Jenis-jenis Segitiga dan Penjelasannya

Bangun Datar: Jenis-jenis Segitiga dan Penjelasannya - Segitiga merupakan sebuah bangun datar yang memiliki tiga titik sudut dengan tiga ruas garis yang mengapitnya. Segitiga memiliki banyak jenis, semua itu dapat dibedakan tergantung panjang sisi juga besar sudutnya.

Rumus-rumus segitiga selalu terikat dengan yang namana Teorema Phytagoras. Materi ini harus sobat kuasai terlebih dahulu sebelum melangkah ke bab ini. Bila sobat belum mengerti materi ini, bisa kunjungi link --> Teorema Phytagoras.

1. Jenis-jenis Segitiga Berdasarkan Panjang Sisinya

a. Segitiga Sama Kaki

Adalah segitiga yang dua sisinya sama panjang.


Panjang AC = BC
∠A = ∠B
∠A + ∠B + ∠C = 180°s

b. Segitiga Sama Sisi

Adalah segitiga yang ketiga sisinya sama panjang.


Panjang AB = BC = AC
∠A = ∠B = ∠C = 60°
∠A + ∠B + ∠C = 180°

c. Segitiga Sembarang

Adalah segitiga yang panjang ketiga sisinya berbeda-beda.


- Ketiga sisinya tidak sama panjang ( AB ≠ BC ≠ AC )
- Ketiga sudutnya tidak sama besar ( ∠A ≠ ∠B ≠ ∠C )
- ∠A + ∠B + ∠C = 180°

2. Jenis Segitiga Berdasarkan Besar Sudutnya

a. Segitiga Siku-siku

Adalah segitiga yang salah satu sudutnya adalah 90°


∠A = 90°
∠B = 45°
∠C = 45°

b. Segitiga Lancip

Adalah segitiga yang besar ketiga sudutnya kurang dari 90°


∠A, ∠B, dan ∠C lebih kecil dari 90°

c. Segitiga Tumpul

Adalah segitiga yang besar salah satu sudutnya lebih dari 90°


∠C lebih besar dari 90°

Mungkin itu saja Jenis-jenis Segitiga dan Penjelasannya yang bisa saya berikan, semoga bermanfaat buat kalian semua.

Aritmetika Sosial: Untung dan Rugi Pengertian & Contoh Soal

Aritmetika Sosial: Untung dan Rugi Pengertian & Contoh Soal - Menurut wikipedia, aritmetika merupakan sebuah cabang ilmu pengetahuan yang memperlajari dasar operasi bilangan. Jadi, aritmetika sosial dapat diartikan sebagai cabang ilmu matematika yang mempelajari matematika pada kehidupan sosial.

Nah, pada kesempatan kali ini, kalian akan disuguhkan materi dasar dari artimetika atau aritmatika sosial yakni menentukan harga penjualan, pembelian, untung dan rugi. Jika harga jual lebih besar dari pada harga beli didapat keuntungan atau laba. Sebaliknya, jika harga jual lebih rendah/kecil dari harga beli maka dinamakan rugi. Harga beli biasa disebut dengan modal.

1

ARITMETIKA SOSIAL

- Untung dan Rugi -

Untung  = Harga penjualan > Harga pembelian
Rugi    = Harga penjualan < Harga pembelian

Besarnya keuntungan = harga jual - harga beli
Besarnya kerugian   = harga beli - harga jual

Contoh Soal 1:

Seorang peternak ayam membeli seekor ayam dengan harga Rp.200.000,-. Kemudian
ayam tersebut dijual dengan harga Rp.250.000,-. Berapa keuntungan yang didapat
peternak tersebut...

Jawab :

Harga beli = Rp.200.000,-
Harga jual = Rp.250.000,-

Besarnya keuntungan = harga jual - harga beli
                    = 250.000    - 200.000
                    = Rp. 50.000,-

Contoh Soal 2:

Seorang pedagang kelinci membeli kelinci lokal sebanyak 100 ekor dengan harga
Rp. 4.000.000,-. Dalam perjalanan, terdapat 10 kelinci yang mati. 30 ekor laku
dijual dengan harga Rp. 50.000,- per ekor, sedangkat sisanya dengan harga
Rp. 40.000,-. Berapa besar keuntungan dan kerugian yang didapat pedagang...

Jawab :

Harga pembelian    = Rp. 4.000.000,-
Harga jual 30 ekor = 30 x Rp. 50.000,- = Rp. 1.500.000,-

Sisa kelinci yang dijual = 100 - 30 - 10 ( 10 kelinci yang mati )
                         = 60 ekor
Harga jual 60 ekor       = 60 x Rp. 40.000,-
                         = Rp. 2.400.000,-

Harga penjualan    = Rp. 2.400.000,- + Rp. 1.500.000,-
                   = Rp. 3.900.000,-

Ternyata harga penjualan < harga pembelian maka pedagang mengalami kerugian.

Besar kerugian     = harga beli - harga jual
                   = 4.000.000  - 3.900.000
                   = Rp. 100.000,-

Mungkin itu saja informasi yang bisa saya berikan tentang Aritmetika Sosial: Untung dan Rugi Pengertian & Contoh Soal semoga bermanfaat.

Materi: Pengertian Dasar Himpunan dan Anggotanya

Materi: Pengertian Dasar Himpunan dan Anggotanya - Dalam arti dasar, himpunan merupakan sekumpulan benda-benda atau objek-objek tertentu yang tercakup dalam satu kesatuan yang memiliki definisi yang jelas.

Untuk menyatakan suatu himpunan, biasa menggunakan huruf kapital D, E, F, dll. Sedangkan untuk menanyakan anggotanya menggunakan huruf kecil a, b, c, d, dll.

Contoh :

A adalah himpunan bilangan asli kurang dari 8
Anggota himpunannya adalah 1,2,3,4,5,6,7
Jadi A = {1,2,3,4,5,6,7}

B adalah himpunan bilangan genap antara 1 sampai 9
Anggota himpunannya adalah 2,4,6,8Jadi B = {2,4,6,8}

A. Anggota Himpunan

Anggota himpunan adalah sebuah benda-benda atau objek yang terdapat disebuah himpunan. Anggota sebuah himpunan dapat dinyatakan dengan notasi ∈ dan jika bukan anggota himpunan dinyatakan dengan notasi ∉.
Dan banyaknya anggota himpunan B dinyatakan dengan n(B).

Contoh :

A adalah himpunan bilangan ganjil antara 2 sampai 12

A = {himpunan bilangan ganjil antara 2 sampai 12} atau A = {3,5,7,9,11}
Maka --> 3 ∈ A, 5 ∈ A, 7 ∈ A, 9 ∈ A, 11 ∈ A
     --> 2 ∉ A, 4 ∉ A, 6 ∉ A, 8 ∉ A, 10 ∉ A, 12 ∉ A

Banyak anggota himpunan A adalah n(A) = 5

B. Menyatakan Suatu Himpunan

Untuk menyatakan sebuah himpunan, dapat dilakukan dengan 3 cara :

a. Menuliskan dengan kata-kata atau syarat keanggotaannya
b. Menuliskan notasi pembentuk himpunan
c. Mendaftarkan anggotanya

NO	Dengan Kata-kata	Notasi Pembentuk Himpunan	Mendaftarkan Anggotanya
1	A adalah himpunan Bilangan genap di bawah 10	A={x|x < 10; x ∈ bilangan genap}	A= {2,4,6,8}
2	B adalah himpunan kelipatan 5 di bawah 20	B={x|x < 20; x ∈ kelipatan 5}	B={5,10,15}

Mungkin itu saja informasi yang bisa saya berikan tentang Materi: Pengertian Dasar Himpunan dan Anggotanya semoga bermanfaat.

Rumus Cepat Barisan dan Deret Matematika Bagian 1

Rumus Cepat Barisan dan Deret Matematika Bagian 1 - Selamat bertemu kembali sobat, kali ini saya akan membagi kumpulan rumus cepat matematika dengan materi Barisan dan Deret. Berhubung jenis soalnya terlalu banyak, maka saya membagi postingan kedalam tiga bagian. Selamat menikmati soalya sobat, dan selamat belajar.

RUMUS CEPAT MATEMATIKA

- Barisan dan Deret -

Soal 1

Nilai dari = .....


A. 180
B. 190
C. 200
D. 210
E. 220

Jawab :

<< ----- INFO SMART ----- >>

Rumus jumlah n suku pertama deret aritmatika adalah
Sn = ½ n (2a + (n – 1)b

Keterangan :
n = banyaknya suku
a = suku pertama
b = beda


<< ----- RUMUS CEPAT ----- >>

Pertama --> Kita tentukan dahulu nilai awal dan akhir
     n = 1              n = 10
       ↓                  ↓
= (2(1) + 10) +....+ (2(10) + 10)
=      12     +....+      30      ( Nilai awal = 12 dan akhir = 30 )

Kedua   --> Gunakan rumus cepatnya


Jadi jawabannya adalah D. 210

Soal 2

Nilai dari = .....

A. 10200
B. 10020
C. 20100
D. 5050
E. 10002

Jawab :

<< ----- RUMUS CEPAT ----- >>
Pertama --> Kita tentukan nilai awal dan akhir
Soal diatas bisa diubah menjadi
     k = 1           k = 100
       ↓               ↓
= (2(1) + 1)+.....+(2(100) + 1)
=      3    +.....+    201          ( Nilai awal = 3 dan akhir = 201 )

Kedua   --> Gunakan rumus cepatnya.


Jadi jawabannya adalah A. 10200

Soal 3

Jumlah n suku pertama deret aritmatika adalah.
Beda deret aritmatika tersebut adalah...

A. -2
B. 2
C. -4
D. 4
E. 5/2

Jawab :

<< ----- INFO SMART ----- >>
Sn = pn2 + qn suatu deret aritmatika, maka beda = 2p


<< ----- RUMUS CEPAT ----- >>


Jadi jawabannya adalah B. 2

Soal 4

Jumlah n suku pertama deret aritmatika adalah Sn = 3n2 - 4n. Suku ke-n dari deret
tersebut adalah...

A. 3n - 8
B. 6n - 2
C. 6n - 5
D. 3n + 8
E. 6n - 7

Jawab :

<< ----- INFO SMART ----- >>
Jumlah koefisien variable untuk jumlah n suku pertama sama dengan jumlah koefisien
variabel untuk suku ke-n.


<< ----- RUMUS CEPAT ----- >>
1. Jumlahkan koefisiennya saja
   Sn = 3n2 - 4n
     = 3 + (-4)
     = -1

2. Pada pilihan jawaban, cari yang nilai koefisiennya = -1
   A. 3n - 8 = 3 + (-8) = -5 --> Salah
   B. 6n - 2 = 6 + (-2) = 4  --> Salah
   C. 6n - 5 = 6 + (-5) = 1  --> Salah
   D. 3n + 8 = 3 + 8    = 11 --> Salah
   E. 6n - 7 = 6 + (-7) = -1 --> Benar

Jadi jawabannya adalah E. 6n - 7

Soal 5

UAN 2003/P-1/No.10
Suatu keluarga mempunyai 6 anak yang usianya pada saat ini membentuk barisan
aritmetika. Jika usia anak ke-3 adalah 7 tahun dan usia anak ke-5 adalah 12 th,
maka jumlah usia enam anak tersebut adalah...

A. 48.5 Tahun
B. 49.0 Tahun
C. 49.5 Tahun
D. 50.0 Tahun
E. 50.5 Tahun

Jawab

<< ----- INFO SMART ----- >>
Suku ke-n deret aritmatika --> Un = a + (n - 1)b
Jumlah n suku pertama      --> Sn = n/2 (2a +(n - 1)b)


<< ----- RUMUS CEPAT ----- >>
1. Mencari BEDA dengan cepat.
   U3 = 7        7 - 12     5
             b = ------- = ---
   U5 = 12       3 - 5      2

2. Mencari U1 atau a dengan substitusi.
   U3 → a + 2b     = 7
      → a + 2(5/2) = 7
      → a + 5      = 7
      → a          = 7 - 5
      → a          = 2

3. Mencari S6 atau jumlah suku ke-n yang dicari.
  S6 = n/2 (2a + (n - 1)b)
     = 6/2 (2(2) + (6 - 1)5/2)
     = 3   (4 + (25/2)
     = 3   (16,5)
     = 49,5

Jadi jawabannya adalah C. 49.5

Soal 6

Suku ke-n suatu deret adalah Un = 4n + 1. Jumlah sepuluh suku pertama adalah...

A. 210
B. 220
C. 230
D. 240
E. 250

Jawab :

<< ----- INFO SMART ----- >>
Jika Un = an + b
    - maka -
Sn = 1/2 an2 +(b + 1/2a)b
        ↓           ↓
     Integral   Jmlh. Koefisien


<< ----- RUMUS CEPAT ----- >>
jumlah = 5
     ┌─˄──┐
Un = 4n + 1
     ↓ Integral
Sn = 2n2 + 3n
     └──˅───┘
   jumlah = 5

S10 = 2(102) + 3(10)
    = 200 + 30
    = 230

Jadi jawabannya adalah C. 230

Soal 7

Sebuah bola pingpong dijatuhkan dari ketinggian 20 meter dan memantul kembali
dengan ketinggian 3/4 kali tinggi sebelumnya. Pemantulan ini berlangsung terus
menerus hingga bola berhenti. Maka jumlah seluruh lintasan bola adalah...

A. 130
B. 140
C. 15
D. 60
E. 80

Jawab :

<< ----- INFO SMART ----- >>
Bola jatuh di ketinggian t , dan memantul sebesar a/b kali tinggi sebelumnya.
Maka jumlah seluruh lintasan bola sampai berhenti adalah :

    b + a
J = ────── t
    b - a


<< ----- RUMUS CEPAT ----- >>
b + a
J = ──────  t
    b - a
    4 + 3
  = ────── 20
    4 - 3
  = 140

Jadi jawabannya adalah B. 140

Mungkin itu saja informasi yang bisa saya berikan tentang Rumus Cepat Barisan dan Deret Matematika Bagian 1 semoga bermanfaat.

Soal & Pembahasan PERTIDAKSAMAAN SMA Kelas X

Soal & Pembahasan PERTIDAKSAMAAN SMA Kelas X - Dimana ada persamaan, pasti disitu ada pertidaksamaannya. Hal ini berlaku juga pada materi matematika. Nah, berawal dari itu saya menulis artikel ini. Materi yang saya bahas adalah pertidaksamaan. Bagi yang ingin menengok atau melihat artikel saya sebelumnya tentang Pertidaksamaan bisa klik --> Materi Pertidaksamaan.

Nah sekarang kita akan menuju link download kumpulan berbagai soal-soal pertidaksamaan, tentunya dengan pembahasannya. Langsung saja klik link dibawah untuk memulai proses pembelajaran.

Download Soal PERTIDAKSAMAAN SMA Kelas X

SOAL PERTIDAKSAMAAN KELAS X SMA   --> Download <--

Download Pembahasan PERTIDAKSAMAAN SMA Kelas X

PEMBAHASAN PERTIDAKSAMAAN KELAS X SMA   --> Download <--

Mungkin itu saja informasi yang bisa saya berikan tentang Soal & Pembahasan PERTIDAKSAMAAN SMA Kelas X semoga bermanfaat dan selamat belajar.

Soal & Pembahasan PERSAMAAN KUADRAT SMA Kelas X

Soal & Pembahasan PERSAMAAN KUADRAT SMA Kelas X - Persamaan kuadrat adalah salah satu materi matematika yang dapat diselesaikan dengan berbagai cara, bahkan dengan menggunakan cara cepat ( biasa digunakan saat ujian nasional ). Untuk menunjang setiap pembelajaran kalian, blog saya memberi solusi dari segala persoalan kalian. Bagi yang ingin melihat materi persamaan kuadrat, sobat bisa klik --> Materi Persamaan Kuadrat.

Dan pada kesempatan kali ini, saya akan membahas beberapa soal juga pembahasannya tentang materi persamaan kuadrat pada bangku SMA kelas X. Bentuk soal adalah softfile dengan format docx dan bisa anda download secara gratis pada link dibawah ini.

Download Soal PERSAMAAN KUADRAT SMA Kelas X

SOAL PERSAMAAN KUADRAT KELAS X SMA   --> Download <--

Download Pembahasan PERSAMAAN KUADRAT SMA Kelas X

PEMBAHASAN PERSAMAAN KUADRAT KELAS X SMA   --> Download <--

Mungkin itu saja informasi yang bisa saya berikan tentang Soal & Pembahasan PERSAMAAN KUADRAT SMA Kelas X semoga bermanfaat buat kalian dan selamat belajar.

Soal & Pembahasan PELUANG SMA Kelas XI

Soal & Pembahasan PELUANG SMA Kelas XI - Selamat datang kembali di blog saya ini, kali ini saya akan membagi informasi mengenai kumpulan soal beserta pembahasan dengan materi pokoknya adalah Peluang. Peluang adalah salah satu materi yang cukup mudah pada matematika. Namun sekali lagi, diperlukan ketelitian dalam mengerakannya.

Berikut ini adalah link download soal-soal peluang dan pembahasannya yang bisa anda unduh secara gratis. Formatnya adalah docx yang bisa dibuka pada versi pada saja. Cukup klik link yang sudah disediakan dan selamat belajar.

Download Soal PELUANG SMA Kelas XI

SOAL PELUANG KELAS XI SMA   --> Download <--

Download Pembahasan PELUANG SMA Kelas XI

PEMBAHASAN PELUANG KELAS XI SMA   --> Download <--

Mungkin itu saja informasi yang bisa saya berikan tentang Soal & Pembahasan PELUANG SMA Kelas XI semoga bermanfaat dan selamat belajar.

Soal & Pembahasan LOGARITMA SMA Kelas X

Soal & Pembahasan LOGARITMA SMA Kelas X - Jumpa lagi sobat pada blog saya ini, dan kali ini kita akan membahas tentang kumpulan soal-soal dan pembahasannya dengan materi Logaritma. Materi logaritma dapat anda temukan pada blog saya ini dengan klik ---> Materi Logaritma.

Berikut ini saya share kumpulan soal dan juga pembahasannya dari materi Logaritma. Perlu sobat ketahui ya, perhatikan soal-soal yang akan sobat unduh nanti, pelajari dengan sungguh-sungguh ya, selamat mendownload dan belajar.

Download Soal LOGARITMA SMA Kelas X

SOAL LOGARITMA KELAS X SMA   --> Download <--

Download Pembahasan LOGARITMA SMA Kelas X

PEMBAHASAN LOGARITMA KELAS X SMA   --> Download <--

Mungkin itu saja sobat informasi yang bisa saya berikan tentang Soal & Pembahasan LOGARITMA SMA Kelas X semoga bermanfaat.

Soal & Pembahasan LIMIT FUNGSI Mat SMA Kelas XI

Soal & Pembahasan LIMIT FUNGSI Mat SMA Kelas XI - Mari-mari belajar dan belajar lagi biat dapat nilai bagus dan disanjung orang tua. Selengkapnya pada blog ini terdapat beberapa materi matematika dan juga latihan soal yang bisa menjadi acuan anda dalam proses belajar mengajar.

Pada kesempatan yang indah ini, waktunya saya hadirkan kumpulan soal-soal beserta kunci pembahasanya. Materi yang diberikan pada kesempatan ini adalah Limit Fungsi. Wah, langsung terngiang dipikiran anda pasti tentang kerumitan atau kejlimetan, haha. Tenang saja sobat, belajar perlahan dan pasti bisa kelak. Nih, langsung diunduh saja soal dan pembahasanya.

Download Soal LIMIT FUNGSI Mat SMA Kelas XI

SOAL LIMIT FUNGSI KELAS XI SMA   --> Download <--

Download Pembahasan LIMIT FUNGSI Mat SMA Kelas XI

PEMBAHASAN LIMIT FUNGSI KELAS XI SMA   --> Download <--

Mungkin itu saja informasi yang bisa saya berikan tentang Soal & Pembahasan LIMIT FUNGSI Mat SMA Kelas XI semoga bermanfaat buat kalian semua.

Soal & Pembahasan FUNGSI INVERS dan KOMPOSISI SMA XI

Soal & Pembahasan FUNGSI INVERS dan KOMPOSISI SMA XI - Ujian Nasional dan Ujian Sekolah semakin dekat, kita harus lebih dini mempersiapkan diri untuk menghadapinya. Jangan panik dulu sobat, soal-soalnya tak serumit yang kita pikirkan kok, tapi jangan digampangkan juga sih.

Untuk menunjang pembelajaran kalian, nih saya berikan jamu anti galau alias kumpulan soal dan pembahasan materi-materi matematika tentunya. Kesempatan kali ini materi yang akan dikupas adalah Fungsi Invers dan Fungsi Komposisi. Langsung saja sobat klik link downloadnya ya, formatnya docx.

Download Soal FUNGSI INVERS dan KOMPOSISI SMA XI

SOAL FUNGSI INVERS dan KOMPOSISI KELAS XI SMA   --> Download <--

Download Pembahasan FUNGSI INVERS dan KOMPOSISI SMA XI

PEMBAHASAN FUNGSI INVERS dan KOMPOSISI KELAS XI SMA   --> Download <--

Mungkin itu saja sobat informasi yang bisa saya berikan tentang Soal & Pembahasan FUNGSI INVERS dan KOMPOSISI SMA XI semoga bermanfaat buat kalian semua.

Soal & Pembahasan DIMENSI TIGA Mat SMA Kelas X

Soal & Pembahasan DIMENSI TIGA Mat SMA Kelas X - Ayo kita belajar dan belajar lagi. Jadikan generasi kita sebagai generasi positif penerus bangsa yang bisa bermanfaat bagi agama dan negara. Materi ataupun soal yang akan saya bahas kali ini adalah Dimensi Tiga. Materi ini sudah singgah pada bangku SMA kelas X.

Berikut saya berikan soal dan pembahasan materi dimensi tiga matematika SMA kelas X. Klik link download dibawah ini dan selamat menikmati. Format dokumen adalah docx.

Download Soal DIMENSI TIGA Matematika SMA Kelas X

SOAL DIMENSI TIGA KELAS X SMA   --> Download <--

Download Pembahasan DIMENSI TIGA Matematika SMA Kelas X

PEMBAHASAN DIMENSI TIGA KELAS X SMA   --> Download <--

Mungkin itu saja informasi yang bisa saya berikan tentang Soal & Pembahasan DIMENSI TIGA Mat SMA Kelas X semoga bermanfaat.

Soal & Pembahasan Bentuk Pangkat dan Akar SMA

Soal & Pembahasan Bentuk Pangkat dan Akar SMA - Berikut ini saya berikan link download soal-soal dan juga pembahasannya dari materi bentuk pangkat dan akar. Diharapkan kalian semua dapat benar-benar memahami materi ini. Tipe soal yang diberikan pun sangat bagus dan mendasar.

Bagi kalian yang ingin mengetahuinya, bisa langsung klik link download dibawah ini! File berikut berformat docx yang bisa dibuka diseri apa saja. Selamat belajar.

Download Soal BENTUK PANGKAT dan AKAR SMA Kelas X/1

SOAL BENTUK PANGKAT & AKAR KELAS X SMA   --> Download <--

Download Pembahasan BENTUK PANGKAT dan AKAR SMA Kelas X/1

PEMBAHASAN BENTUK PANGKAT & AKAR KELAS X SMA   --> Download <--

Mungkin itu saja informasi yang bisa saya berikan tentang Soal & Pembahasan Bentuk Pangkat dan Akar SMA semoga bermanfaat.